|
The traditional Mandelbrot is created by considering the behavour
of the series zn+1 = zn2 + zo
for each position zo on the complex plane. A more general
equation might be zn+1 = znM + zo.
The resulting shapes are rarely seen, a graphical exploration
of M space is given below.
Integer powers

zn+1 = zn1 + zo
This is of course hardly very interesting, nor fractal.
|

zn+1 = zn2 + zo
The traditional Mendelbrot, M = 2.
|

zn+1 = zn3 + zo
|

zn+1 = zn4 + zo
In general there are M-1 main lobes which result in M-1 degrees of
rotational symmetry.
|

zn+1 = zn5 + zo
|

zn+1 = zn6 + zo
|

zn+1 = zn7 + zo
|

zn+1 = zn8 + zo
|

zn+1 = zn10 + zo
The shapes get increasingly circular looking, but the detail on zooming
in remains fractal..
|
Non-Integer powers

zn+1 = zn2.1 + zo
|

zn+1 = zn2.3 + zo
|

zn+1 = zn2.5 + zo
Real valued M tend to appear like transitions between the lower and
higher integer powers with a split along the negative real axis.
|

zn+1 = zn2.7 + zo
|
Non-Integer powers
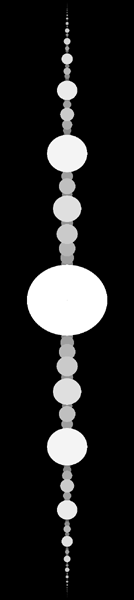
zn+1 = zn-1 + zo
|

zn+1 = zn-2 + zo
|

zn+1 = zn-3 + zo
|

zn+1 = zn-10 + zo
|

zn+1 = zn-2.3 + zo
|

zn+1 = zn-2.5 + zo
|

zn+1 = zn-2.7 + zo
|
|



















